버티의 블로그
[강화학습 #05] λ-returns on TD 본문
n-Step Prediction and Return

4장에서본 TD는 바로 다음 시점인 t+1에서의 reward와 state value만을 TD Target으로 설정해서 state value를 업데이트 했다. 사실 이 방식은 1 step마다 state value를 업데이트 하는 1-step TD방식이었고, 이 step을 n만큼 늘려 적용할 수 있는데 이를 n-step TD라고 한다. 예를 들어, 3-step TD는 3 step마다 업데이트를 진행하며, t+3까지의 상황을 고려한다.

만약 무한히 가는 n-step TD로 확장하면 MC와 거의 동일하게 된다. 따라서 n-step TD를 일반화 하면 위와 같이 MC의 식과 거의 유사해진다.

그래서 n-step TD에서는 적당한 n값을 설정해주는 것이 중요한데, 만약 n값이 너무 커지게 되면 error rate도 증가하는 것을 확인할 수 있다. 위에서는 n이 2나 4정도일 때가 가장 이상적인 그래프를 보인다.

이제 우리는 위 사진처럼 가장 결과가 좋았던 n-step들을 모두 반영하고 싶은 것이다. 2-step일때의 return과 4-step일때의 return을 평균화하여 state value를 업데이트 하고자 한다. 여러 시점에서의 정보를 결합하면 더 정확하게 state value를 추정할 수 있기 때문이다. 그래서 λ-return이라는 개념이 등장한다.
λ-Return
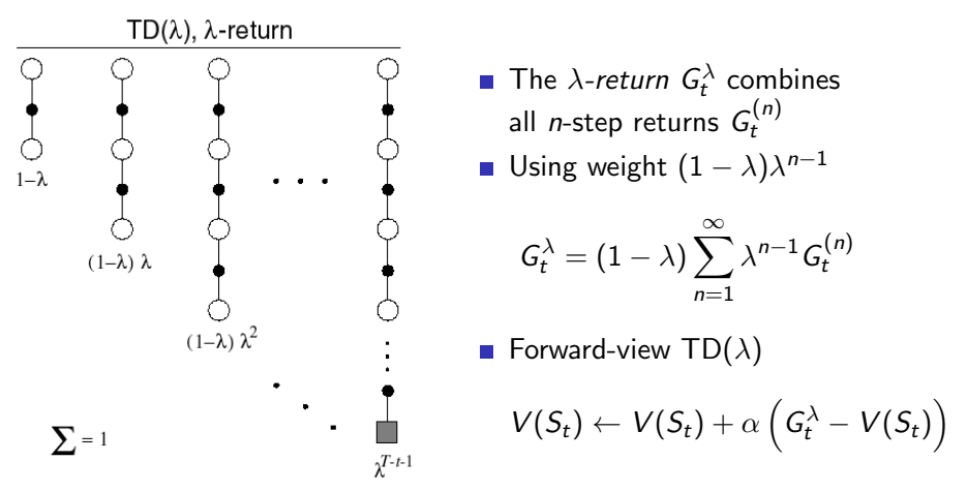
λ-return은 모든 n-step까지의 return을 결합하여 state value를 업데이트하는 방식이다. 이때 기존에 n값이 커질 때 오류가 증가하는것을 방지하기 위해 0과 1사이인 λ를 사용한다. 이로 인해 TD의 장점과 MC의 장점이 결합될 수 있게 되고, 이 방식을 TD(λ) = TD lambda라고 한다.
- λ = 0 : 기존 TD와 동일하게 1-step만을 고려하여 state value를 업데이트한다.
- λ = 1 : 기존 MC와 동일하게 전체 에피소드를 고려하여 state value를 업데이트한다.
- 이 λ값을 0에 가까우면 근접한 step의 return에 더 많은 가중치가 부여되고, 1에 가까울수록 고르게 반영되는 것이다.

TD lambda는 2가지 관점이 존재하는데, 우선 Forward View에서는 MC와 동일하게 n-step까지 도달한 후에 지금까지 얻어낸 return들을 가중 평균화하여 λ-return을 구하고 이를 사용해 state value를 업데이트한다. 식은 위의 TD lambda concept 그림에 있던 식이다. 이렇게 한번에 업데이트하는 방식을 Offline Update라고 한다.

반대로 Backward View에서는 각 state의 Eligibility Trace값을 사용하여 각 step마다 state value를 실시간으로 업데이트한다. 이런 방식을 Online Update라고 한다. t+1에서의 reward(R_t+1)와 state(V(S_t+1))를 이용하여 TD error를 구한 다음, t+1에서의 Eligibility Trace값과 learning rate를 곱한 값을 V(s)에 더하여 state value를 갱신한다. Eligibility Trace 값은 다음과 같이 정의한다.
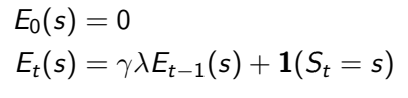
- 여기서 만약 λ가 0이면 E(s)값은 1이 되고, V(s)는 TD error만으로 state value를 업데이트하므로 기존 1-step TD와 같아지는 것이다. 그래서 이를 TD(0)이라고 부르기도 한다.
- 만약 λ가 1이면 아래와 같이 식을 풀어 쓸 수 있고 결국 MC와 같아지게 된다.

이때 E(s)값을 해석하자면, k시점이 s라는 state에 도달한 시점이고, 만약 k시점보다 이전이면 state s에 도달하지 않은 상황으로 고려하여 이 값을 0으로 설정해서 총 계산에 반영하지 않게 하고, 방문했으면 방문한 시점이 얼마나 멀어졌는지를 따진다. k 시점에서 멀어질수록 제곱수인 t-k값은 커질 것이고, 0과 1사이인 discount factor값은 더 작아지게 되어 반영을 덜한다.
이제 이것을 TD lambda에 적용시켜 일반화 하면 다음과 같은 결론이 나온다.

'AI > 강화학습' 카테고리의 다른 글
| [강화학습 #07] SARSA and Q-Learning (0) | 2024.06.05 |
|---|---|
| [강화학습 #06] Model-Free Control (0) | 2024.06.04 |
| [강화학습 #04] Monte-Carlo and Temporal-Difference (0) | 2024.05.19 |
| [강화학습 #03] MDP Planning (0) | 2024.05.19 |
| [강화학습 #02] Markov Decision Process (0) | 2024.05.19 |




