[강화학습 #02] Markov Decision Process

Markov Decision Process

기존 MRP는 상태 전이가 확률적으로만 결정됐지만, MDP는 에이전트가 행동을 선택하는 것을 추가하여 이에 따른 상태 변화와 보상이 달라지는 환경을 뜻한다. MDP는 아래 4가지 요소로 구성된다.

• S : 에이전트의 상태
• A : 에이전트가 취할 수 있는 모든 가능한 action
• P : 특정 s에서 특정 a를 취했을 때 다음 s로 전이될 확률, P(s′∣s,a)가 이 의미이다.
• R : 특정 s에서 특정 a를 취했을 때 받는 보상, R(s,a,s′)로 표기한다.
• π : 에이전트가 행동을 결정하는 규칙으로, 상태 s에서 행동 a를 선택할 확률을 π(a∣s)로 나타낸다.

---

Bellman Expectation Equation

1장에서 살펴본 state value function은 특정 state에서 시작해서 해당 π를 따랐을 때 에이전트가 기대할 수 있는 보상의 총합으로, V_π(s)로 표기했다. MDP는 여기에 action 개념을 추가하여 Action Value Function을 사용한다. 이를 다시 말하면, 상태 s에서 행동 a를 취하고 π를 따랐을 때 에이전트가 기대할 수 있는 보상의 총합이고, Q_π(s,a)로 표기한다. 이 값을 사용하는 대표적인 식이 Bellan Expectaion Equation이다.

 

여기서 V(s)와 Q(s, a) 다음과 같이 정의한다.

V(s) 기준으로 설명하자면, 상태 s에서 특정 π를 따를 때 다음 시간인 t+1에서 얻는 보상과 state value를 더한다. 그리고 이 계산이 가능한 모든 값을 평균내어 계산한 값이 벨만 방정식에서의 V(s)이고, action을 추가하면 Q(s, a)이다. 이 과정이 재귀적으로 계속 반복되면서 state-action value function이 정의되는 것이다.

Bellman Equation for state value function

 

 

왼쪽 그림에서는 V(s)가 각 행동 a의 Q(s, a)와 π를 따를 때 그 a를 선택할 확률인 π(a|s)의 가중합임을 나타내는데, Q(s, a)를 벨만 방정식의 정의로 풀어쓴 것이 오른쪽 그림이다. 

Bellman Equation for action value function

 

마찬가지로 벨만 방정식에서의 Q(s, a) 정의에서 V(s)를 벨만 방정식의 정의로 풀어쓰면 오른쪽 그림과 같다.

Find state value using Bellman Equation

 

위 예시에서, 빨간색 원의 V(s)가 7.4가 나오게된 이유를 설명하자면 다음과 같다.

• 모든 state 전이 확률은 0.5, discount factor은 1로 가정.
• 우선 공부를 하면 가능한 state가 하나고, 리워드는 10이며, 해당 s의 V(s)는 0이다.
• 따라서 0.5 * (10 + 1 * (1 * 0)) = 5
• 술집을 가면 가능한 state가 3개이므로 세 경우를 모두 계산해준다.
  
  • 리워드 : 1
  • 첫번째 경우 : 0.2 * (-1.3) = - 0.26
  • 두번째 경우 : 0.4 * 2.7 =  1.08
  • 세번째 경우 : 0.4 * 7.4 = 2.96
• 따라서 0.5 * (1 + 1 * (- 0.26 + 1.08 + 2.96)) = 2.39
• 이 둘을 더하면 최종 V(s)가 된다. 5 + 2.39 = 7.39 -> 약 7.4

Find optimal action value on optimal value situation

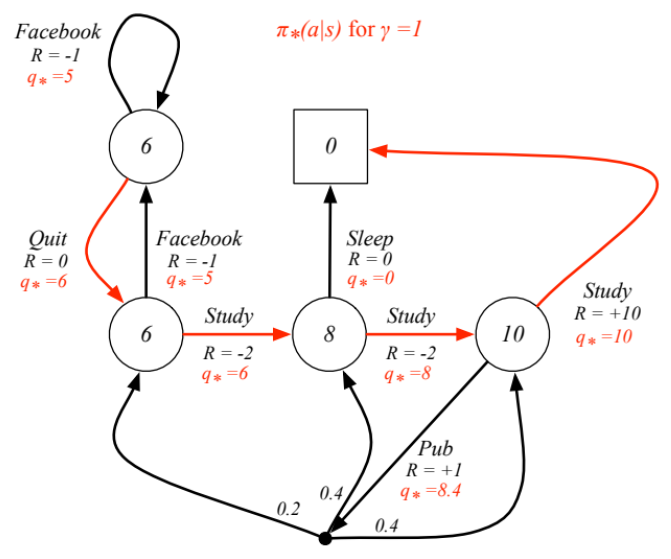
각 state에서 가능한 Q(s, a)중 가장 optimal(max)한 값을 q*로 정리하면 위와 같다. 이렇게 Bellman equation에 optimality를 적용해서 최적의 action을 선택할 수 있고 바로 Optimal policy를 구할 수 있게 된다. 이 식을 Bellman Optimal Equation이라 한다.

 

Bellman Optimal Equation for state and action value function

 

Optimal policy for above example