버티의 블로그
[강화학습 #08] Value Function Approximation 본문
앞장에서 본 SARSA와 Q-Learning는 Table로 만들어서 값을 기억하는 방법이라 할 수 있는데, 현실은 continuous state space이기에 state가 거의 무한대에 가까우므로 수용할 메모리도 부족하고 계산도 기하급수적으로 복잡해진다. 따라서 이제부터는 value function의 근사값을 사용하고자 한다.
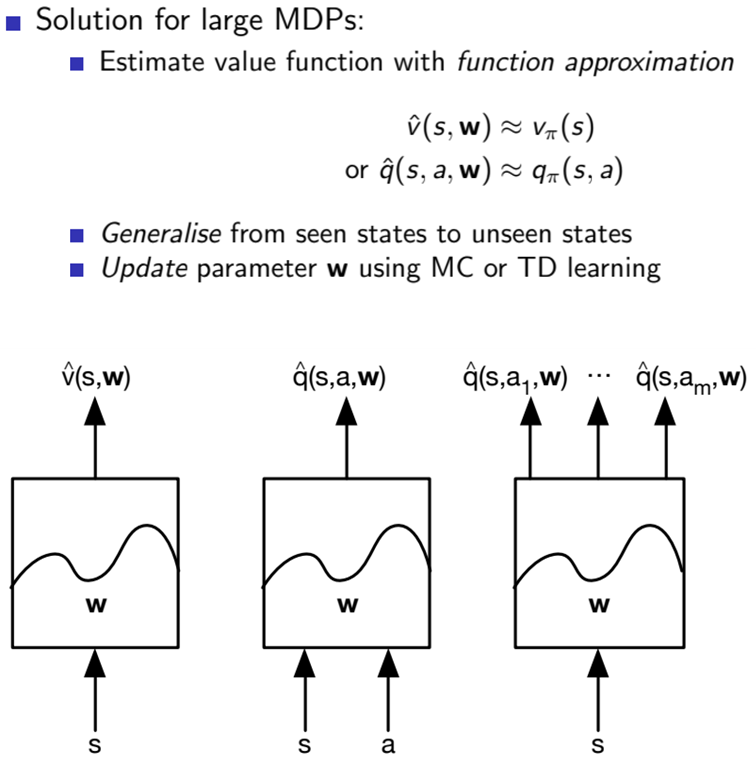
그래서 이제는 w라는 새로운 변수로 value function 값을 함수화하는 것이다. 그림으로 다시 보면, w라는 파라메터로 조정되는 함수가 state나 action값을 받아 근사값을 출력해낸다. 그래서 앞으로는 학습을 통해 Q function을 업데이트 하는 것이 아닌 w를 업데이트를 하게 된다. 여기서 업데이트를 하는 방식은 Gradient Descent이다.

Gradient Descent는 local minimum을 찾아가는 알고리즘이다. 여기서는 실제 값인 Vπ(s)와 근사 값인 V^(S, w)의 차이(error)를 줄여나가는데, 이때 이 둘의 차이를 Mean Squared Error(MSE) 손실 함수로 정의하고, w에 대해 미분해보며 local minimum을 찾는다.

이때 기댓값은 sampling을 통해 얻어야 하는데, 여기서도 Stochastic Gradient Descent로 전체 데이터셋을 사용하는 대신 무작위로 선택된 데이터 하나만 사용해서 기울기를 계산하고 파라메터를 업데이트하여 sampling을 할 수 있다.

또한 여기서 learning target에 해당하는 Vπ(S)를 각각 MC, TD(0), TD(λ) 방법으로 치환해주면 각 학습 방식에서 사용되는 sampling 식을 위와 같이 얻어낼 수 있다. 다시 말해, △w만큼 파라메터를 업데이트하게 되는 것이다.

이때 V^(S, w)를 state s의 모든 feature 벡터들의 linear combination으로 나타낼 수 있는데, 이를 미분하면 feature value만 남는다. 이를 이용해서 아래처럼 식 변형이 가능하다.

여태 V^(S, w)만 다뤘지만, 동일하게 action value function도 approximation해서 사용할 수 있다. 식만 아래와 같이 바꾸면 되고 나머지는 위에서 V^(S, w) 대신 q^(S, A, w)만 써주면 완전히 같다.

Batch RL and Experience Replay

에이전트가 경험해서 얻은 training(experience) data set을 D라고할 때, 기존 SGD에서 이를 활용하는 방법은 위와 같았다. D에서 임의의 state와 value(π) 쌍을 선택하고 그 쌍으로 SGD 업데이트를 적용해서 파라메터 w를 업데이트하고 이 오차값을 최소화하는 w를 찾았다.
그러나 이 방법은 데이터를 비효율적으로 사용한다 볼 수 있는데, 선택된 데이터 쌍은 SGD로 한번 업데이트 후 재사용되지 않고 바로 버려지기 때문이다. 그래서 계속해서 새로운 데이터 쌍을 찾기 위해 데이터가 많이 필요하다.


이런 비효율성을 개선하기 위해 강화학습에 batch 방식을 적용한 Batch Reinforce Learning이 등장하였다. 여기에는 핵심 개념인 Experience Replay가 들어가는데 이 특징은 다음과 같다.
- 에이전트가 특정 시간만큼 환경과 상호작용할때마다 (state, action, reward, next state) 쌍을 D에 저장
- batch size 만큼 D에서 데이터 쌍을 무작위로 가져와서 사용
- 사용한 데이터셋을 버리지 않고 반복적으로 재사용
그래서 데이터 효율성이 기존보다 훨씬 증가하게 되고, 이를 Q-Learning에 적용한 방법이 바로 Deep Q-Networks(DQN)인 것이다. 이 DQN에 대해서는 다음 장에서 더 자세히 알아볼 것이다.
'AI > 강화학습' 카테고리의 다른 글
| [강화학습 #09] Policy Gradient (1) | 2024.06.13 |
|---|---|
| [강화학습 #07] SARSA and Q-Learning (0) | 2024.06.05 |
| [강화학습 #06] Model-Free Control (0) | 2024.06.04 |
| [강화학습 #05] λ-returns on TD (0) | 2024.05.20 |
| [강화학습 #04] Monte-Carlo and Temporal-Difference (0) | 2024.05.19 |




